Alternating Current-Test Papers

 CBSE Test Paper-01

Class - 12 Physics (Alternating Current)

---

1. A 200 ohm resistor is connected in series with a 5μF$5\mu F$ capacitor. The voltage across the resistor is VR = (1.20 V) cos(2500 rad/s)t.Capacitive reactance is

   1. 70 Ω$\mathrm{\Omega }$
   2. 80 Ω$\mathrm{\Omega }$
   3. 60 Ω$\mathrm{\Omega }$
   4. 90 Ω$\mathrm{\Omega }$
2. The current in a series LCR circuit will be maximum, then ω$\omega$ is:

   1. as large as possible
   2. LC−−−√$\sqrt{LC}$
   3. LCR−−−−√$\sqrt{LCR}$
   4. equal to natural frequency of LCR system
3. A series circuit consists of an ac source of variable frequency, a 115.0 Ω$\mathrm{\Omega }$ resistor, a 1.25 μF$\mu \mathrm{F}$ capacitor, and a 4.50-mH inductor. Impedance of this circuit when the angular frequency of the ac source is adjusted to twice the resonant angular frequency is

   1. 146.0 Ω$\mathrm{\Omega }$
   2. 176.0 Ω$\mathrm{\Omega }$
   3. 166.0 Ω$\mathrm{\Omega }$
   4. 156.0 Ω$\mathrm{\Omega }$
4. For high frequency capacitor offers:

   1. Less resistance
   2. More resistance
   3. None of these
   4. Zero resistance
5. Effective voltage Vrms is related to peak voltage Vo by

   1. Vrms = 0.707 Vo
   2. Vrms = 0.787Vo
   3. Vrms = 0.9 Vo
   4. Vrms = 0.5 Vo
6. An AC current, I = I0 sin ωt$\omega t$ produces certain heat H in a resistor R over a time T=2π/ω$T=2\pi /\omega$. Write the value of the DC current that would produce the same heat in the same resistor in the same time.

7. Define the term rms value of the current. How is it related to the peak value?

8. Define the term wattless current.

9. The figure shows a series L-C-R circuit connected to a variable frequency 250 V source with L = 50 mH, C = 80μ$\mu$F and R = 40Ω$\mathrm{\Omega }$ .
   

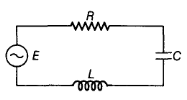
   1. the source frequency which drives the circuit in resonance.
   2. the quality factor (Q) of the circuit.

10. The number of turns in secondary coil of a transformer is 100 times the number of turns in the primary coil. What is the transformation ratio?

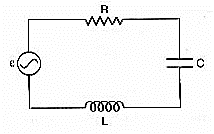
11. In the following circuit, calculate,

    1. the capacitance 'c' of the capacitor if the power factor of the circuit is unity, and
    2. also calculate the Q-factor of the circuit.
       

12. A source of AC voltage V = V0 sin ωt$\omega t$ is connected to a series combination of a resistor 'R' and a capacitor 'C'. Draw the phasor diagram and use it to obtain the expression for

    1. impedance of the circuit and
    2. phase angle.
13. 1. For a given AC, i = im sin ωt$\omega t$ , show that the average power dissipated in a resistor R over a complete cycle is 12i2mR$\frac{1}{2}{i}_m^{2}R$.
    2. A light bulb is rated at 100 W for a 220V AC supply. Calculate the resistance of the bulb.

14. An LC circuit contains a 20 mH inductor and a 50μF$50\mu F$ capacitor with an initial charge of 10 mC. The resistance of the circuit is negligible. Let the instant the circuit is closed be t = 0.

    1. What is the total energy stored initially? Is it conserved during LC oscillations?
    2. What is the natural frequency of the circuit?
    3. At what time is the energy stored
       1. completely electrical (i.e. stored in the capacitor)?
       2. completely magnetic (i.e. stored in the inductor)?
    4. At what times is the total energy shared equally between the inductor and the capacitor?
    5. If a resistor is inserted in the circuit, how much energy is eventually dissipated as heat?

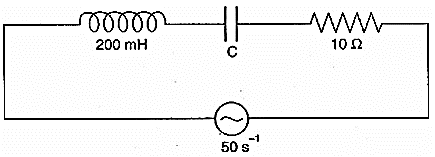
15. A series of LCR circuit connected to a variable frequency 230 V source, L = 5.0 H, C=80μF$C=80\mu F$, R=40Ω$R=40\mathrm{\Omega }$
    

    1. Determine the source frequency which drives the circuit in resonance.
    2. Obtain the impedance of the circuit and the amplitude of current at the resonating frequency.
    3. Determine the rms potential drops across the three elements of the circuit. Show that the potential drop across the LC combination is zero at the resonating frequency.

CBSE Test Paper-01
Class - 12 Physics (Alternating Current)
Answers

---

1. 2. 80Ω$\mathrm{\Omega }$
      Explanation: VR = (1.20 V) cos(2500 rad/s)t
      ω=2500rad/s$\omega =2500rad/s$
      C=5μF=5×10−6F$C=5\mu F=5\times {10}^{-6}F$
      Capacitive reactance
      XC=1ωC=12500×5×10−6=80Ω$X_C=\frac{1}{\omega C}=\frac{1}{2500\times 5\times {10}^{-6}}=80\mathrm{\Omega }$
2. 4. equal to natural frequency of LCR system
      Explanation: for maximum current in LCR series circuit impedance Z will be minimum
      i=EZ$i=\frac{E}{Z}$
      Z=R2+(XL−XC)2−−−−−−−−−−−−−−√$Z=\sqrt{R^2+{(X_L-X_C)}^2}$
      impedance Z will be minimum when XL=XC$X_L=X_C$
      hence
      ωL=1ωC$\omega L=\frac{1}{\omega C}$
      ω=1LC√$\omega =\frac{1}{\sqrt{LC}}$
      this is equal to natural frequency of LCR system
3. 1. 146.0
      Explanation: R=115Ω$R=115\mathrm{\Omega }$
      C=1.25μF=1.25×10−6F$C=1.25\mu F=1.25\times {10}^{-6}F$
      L=4.5mH=4.5×10−3H$L=4.5mH=4.5\times {10}^{-3}H$
      resonant angular frequency
      ω0=1LC√=14.5×10−3×1.25×10−6√=17.5×10−5${\omega }_0=\frac{1}{\sqrt{LC}}=\frac{1}{\sqrt{4.5\times {10}^{-3}\times 1.25\times {10}^{-6}}}=\frac{1}{7.5\times {10}^{-5}}$
      given that the angular frequency of the ac source ω=2ω0=27.5×10−5=26666.6rad/s$\omega =2{\omega }_0=\frac{2}{7.5\times {10}^{-5}}=26666.6rad/s$
      impedance
      Z=R2+(ωL−1ωC)2−−−−−−−−−−−−−−√$Z=\sqrt{R^2+{\left(\omega L-\frac{1}{\omega C}\right)}^2}$
      =1152+[(26666.6×4.5×10−3)−(126666.6×1.25×10−6)]2−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−√$=\sqrt{{115}^2+{\left[(26666.6\times 4.5\times {10}^{-3})-\left(\frac{1}{26666.6\times 1.25\times {10}^{-6}}\right)\right]}^2}$
      Z=146Ω$Z=146\mathrm{\Omega }$
4. 1. Less resistance
      Explanation: capacitive reactance
      XC=1ωC=12πfC$X_C=\frac{1}{\omega C}=\frac{1}{2\pi fC}$
      XC∝1C$X_C\propto \frac{1}{C}$
      hence, for high frequency capacitor offers less resistance.
5. 1. Vrms = 0.707 Vo
      Explanation: Average value of V2 over a complete cycle is given by

      V¯2=1T∫T0V2dt${\overline{V}}^2=\frac{1}{T}{\int }_0^T{V}^{2}dt$
      V=Vosinωt$V=V_o\sin \omega t$
      T=2πω$T=\frac{2\pi }{\omega }$
      V¯2=ω2π∫2π/ω0Vo2sin2ωtdt=${\overline{V}}^2=\frac{\omega }{2\pi }{\int }_0^{2\pi /\omega }{V_o}^2{\sin }^2\omega tdt=$ ω2πVo2∫2π/ω0(1−cos2ωt)2dt$\frac{\omega }{2\pi }{V_o}^2{\int }_0^{2\pi /\omega }\frac{\left(1-\cos 2\omega t\right)}{2}dt$
      V¯2=ω2πVo22[t−sin2ωt2ω]2π/ω0${\overline{V}}^2=\frac{\omega }{2\pi }\frac{{V_o}^2}{2}{\left[t-\frac{\sin 2\omega t}{2\omega }\right]}_0^{2\pi /\omega }$ =ω2πVo22(2πω)$=\frac{\omega }{2\pi }\frac{{V_o}^2}{2}\left(\frac{2\pi }{\omega }\right)$
      V¯2=V202${\overline{V}}^2=\frac{V_0^2}{2}$
      The root-mean-square value of the alternating voltage is given by
      Vrms=V¯2−−−√=Vo2√$V_{rms}=\sqrt{{\overline{V}}^2}=\frac{V_o}{\sqrt{2}}$
      Vrms = 0.707 V0

6. Heat produced by DC is H = I2RT ....(i)
   Heat produced by AC is
   H=I2VRT or H=(I02√)2RT$H=I_V^{2}RT\text{ or }H={\left(\frac{I_0}{\sqrt{2}}\right)}^{2}RT$ ....(ii)

   Where IV = I0/2–√$\sqrt{2}$ = rms value of the AC current
   From Eqs. (i) and (ii), we get
   I2RT=I20RT2 or I=I0/2–√$I^{2}RT=\frac{I_0^{2}RT}{2}\text{ or }I=I_0/\sqrt{2}$
   where I stands for DC and I0 is the peak value of AC current.

7. It is defined as the value of Alternating Current (AC) over a complete cycle which would generate same amount of heat in a given resistor that is generated by steady current in the same resistor and in the same time during a complete cycle. It is also called virtual value or effective value of AC.
   Let the peak value of the current be I0
   ∴Irms=I02√⇒Irms=I02√$\therefore I_{rms}=\frac{I_0}{\sqrt{2}}\Rightarrow I_{rms}=\frac{I_0}{\sqrt{2}}$
   Where, I0 peak value of AC.

8. The current in an AC circuit is said to be Wattless Current when the average power consumed in such circuit corresponds to Zero.Such current is also called as Idle Current.

9. Given, L = 50mH = 50×10−3H$50\times {10}^{-3}H$
   C=80μF=80×10−6F$C=80\mu F=80\times {10}^{-6}F$
   R=40Ω,V=200V$R=40\mathrm{\Omega },V=200V$

   1. In the L-C-R, the resonant angular frequency when XL= XC
      ω0=1LC√=150×10−3×80×10−6√=500rad/s${\omega }_0=\frac{1}{\sqrt{LC}}=\frac{1}{\sqrt{50\times {10}^{-3}\times 80\times {10}^{-6}}}=500\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}$
      ω=2πv⇒v=ω2π$\omega =2\pi v\Rightarrow v=\frac{\omega }{2\pi }$
      ⇒v=5002π=250π=79.61≈80Hz$\Rightarrow v=\frac{500}{2\pi }=\frac{250}{\pi }=79.61\approx 80\mathrm{H}\mathrm{z}$
   2. Quality factor, Q=ω0LR=500×50×10−340=0.625$Q=\frac{{\omega }_{0}L}{R}=\frac{500\times 50\times {10}^{-3}}{40}=0.625$

10. Transformation ratio
    ⇒k=NsNp$\Rightarrow k=\frac{N_s}{N_p}$
    Since Ns=100×Np$N_s=100\times N_p$
    Thus k=100NpNp=100$k=\frac{100N_p}{N_p}=100$

11. 1. Power factor, cosϕ=RZ$\cos \varphi =\frac{R}{Z}$ or Z = R [For power factor unity cosθ=1$\cos \theta =1$]
       ∴XC=XL$\therefore X_C=X_L$ or 12πfC=2πfL$\frac{1}{2\pi fC}=2\pi fL$
       or C=14π2f2L=14×9.87×(50)2×200×10−3$C=\frac{1}{4{\pi }^2{f}^{2}L}=\frac{1}{4\times 9.87\times {(50)}^2\times 200\times {10}^{-3}}$
       =5×10−5F$=5\times {10}^{-5}F$
       or C=50μF$C=50\mu F$
    2. Q-factor =1RLC−−√$=\frac{1}{R}\sqrt{\frac{L}{C}}$
       Q=110200×10−35×10−5−−−−−−√=6.32$Q=\frac{1}{10}\sqrt{\frac{200\times {10}^{-3}}{5\times {10}^{-5}}}=6.32$
12. 1. V=V0sinωt$V=V_0\sin \omega t$
       From diagram, by parallelogram law of vector addition, VR + VC = V
       Using pythagorean theorem,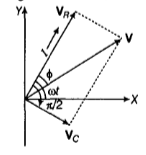
       
       We get
       V2=V2R+V2C=(IR)2+(IXC)2⇒V2=I2(R2+X2C)$V^2=V_R^2+V_C^2=(IR{)}^2+{\left(I{X}_C\right)}^2\Rightarrow V^2=I^2\left(R^2+X_C^2\right)$, XC and R being the capacitive reactance and resistance of the resistor respectively.
       ∴I=V/R2+X2C−−−−−−−√=V/Z$\therefore I=V/\sqrt{R^2+X_C^2}=V/Z$ (say) where, Z = R2+X2C−−−−−−−√=R2+1/ω2C2−−−−−−−−−−−√$\sqrt{R^2+X_C^2}=\sqrt{R^2+1/{\omega }^2{C}^2}$
       Z = impedance of the circuit.
    2. The phase angle ϕ$\varphi$ between resultant voltage and current is given by
       tanϕ=VCVR=IXCIR=XCR=1/ωCR=1ωRC$\tan \varphi =\frac{V_C}{V_R}=\frac{I{X}_C}{IR}=\frac{X_C}{R}=\frac{1/\omega C}{R}=\frac{1}{\omega RC}$ ⇒$\Rightarrow$ ϕ=$\varphi =$ tan-1(1ωRC$\frac{1}{\omega RC}$)
13. 1. The average power dissipated,
       P¯¯¯¯=(i2R)=(i2mRsin2ωt)=i2mR(sin2ωt)$\overline{P}=\left(i^{2}R\right)=\left(i_m^{2}R{\sin }^2\omega t\right)=i_m^{2}R\left({\sin }^2\omega t\right)$
       ∵sin2ωt=12(a−cos2ωt)$\because {\sin }^2\omega t=\frac{1}{2}(a-\cos 2\omega t)$
       ∴(sin2ωt)=12[1−(cos2ωθ)]=12(∵cos2ωt=0)$\therefore \left({\sin }^2\omega t\right)=\frac{1}{2}[1-(\cos 2\omega \theta )]=\frac{1}{2}(\because \cos 2\omega t=0)$
       ∴P¯¯¯¯=12i2mR$\therefore \overline{P}=\frac{1}{2}{i}_m^{2}R$
    2. ) Power of the bulb P = 100 W

    voltage, V = 220 V
    R=V2P=(220)2100=484Ω$R=\frac{V^2}{P}=\frac{(220{)}^2}{100}=484\mathrm{\Omega }$

14. 1. Total initial energy
       E=Q202C=10−2×10−22×50×10−6J$E=\frac{Q_0^2}{2C}=\frac{{10}^{-2}\times {10}^{-2}}{2\times 50\times {10}^{-6}}J$ = 1 J
       This energy shall remain conserved in the absence of resistance.
    2. Angular frequency, ω=1LC√$\omega =\frac{1}{\sqrt{LC}}$
       =1(20×10−3×50×10−6)1/2Hz$=\frac{1}{{(20\times {10}^{-3}\times 50\times {10}^{-6})}^{1/2}}Hz$
       = 103 rads-1
       v=1032πHz=159Hz$v=\frac{{10}^3}{2\pi }Hz=159Hz$
    3. Q=Q0cosωt$Q=Q_0\cos \omega t$
       Or Q=Q0cos2πTt$Q=Q_0\cos \frac{2\pi }{T}t$, where T=1v=1159s$T=\frac{1}{v}=\frac{1}{159}s$ = 6.3 ms
       Energy stored is completely electrical at t = 0, T/2, 3T/2 . . .
       Electrical energy is zero i.e. energy stored is completely magnetic at
       t=T4,3T4,5T4,...$t=\frac{T}{4},\frac{3T}{4},\frac{5T}{4},...$
    4. At t=T8,3T8,5T8,...$t=\frac{T}{8},\frac{3T}{8},\frac{5T}{8},...$ [∵Q=Q0cosωT8=Q0cosπ4=Q02√]$\left[\because Q=Q_0\cos \frac{\omega T}{8}=Q_0\cos \frac{\pi }{4}=\frac{Q_0}{\sqrt{2}}\right]$
       ∴$\therefore$ Electrical energy =Q22C=12Q202C$=\frac{Q^2}{2C}=\frac{1}{2}\frac{Q_0^2}{2C}$, which is half of the total energy.
    5. R damps out the LC oscillations eventually. The whole of the initial energy 1.0 J is eventually dissipated as heat.

15. Here, L = 5.0 H, R=40Ω$R=40\mathrm{\Omega }$
    C=80μF=80×10−6F$C=80\mu F=80\times {10}^{-6}F$
    Ev = 230 volt
    E0=0–√Ev=2–√×230V$E_0=\sqrt{0}{E}_v=\sqrt{2}\times 230V$

    1. Resonance angular frequency,
       ωr=1LC√$\omega r=\frac{1}{\sqrt{LC}}$
       =15×80×10−6√=12×10−7$=\frac{1}{\sqrt{5\times 80\times {10}^{-6}}}=\frac{1}{2\times {10}^{-7}}$ = 50 rad/sec = 50 rad/sec.
    2. Impedance Z=R2+(ωL−1ωC)2−−−−−−−−−−−−−−√$Z=\sqrt{R^2+{\left(\omega L-\frac{1}{\omega C}\right)}^2}$
       At resonance, ωL=1ωC$\omega L=\frac{1}{\omega C}$
       Z=R2−−−√=R=40Ω$Z=\sqrt{R^2}=R=40\mathrm{\Omega }$
       Amplitude of current at resonating frequency
       I0=E0z=2√×23040$I_0=\frac{E_0}{z}=\frac{\sqrt{2}\times 230}{40}$ = 8.13 amp
       Iv=I02√=8.132√=5.75amp$I_v=\frac{I_0}{\sqrt{2}}=\frac{8.13}{\sqrt{2}}=5.75amp$
    3. Potential drop across L
       VLrms=IvωrL=5.75×50×5.0$V_{Lrms}=I_v{\omega }_{r}L=5.75\times 50\times 5.0$ = 1437.5 V
       Potential drop across R
       VRrms=Iv×R=5.75×40$V_{Rrms}=I_v\times R=5.75\times 40$ = 230 volt
       Potential drop across C
       VCrms=Iv(1ωrC)$V_{Crms}=I_v(\frac{1}{{\omega }_{r}C})$
       =5.75×150×80×10−6$=5.75\times \frac{1}{50\times 80\times {10}^{-}6}$
       =5.754×103$=\frac{5.75}{4}\times {10}^3$ = 1437.5 V
       Potential drop across LC circuit
       VLCrms=​​VLrms−VCrms=0