Electric Charges and Fields-Revision Notes

 CBSE Class 12 Physics

Revision Notes
Chapter-1
Electric Charges and Fields

---

• Like Charges and Unlike Charges: Like charges repel and unlike charges attract each other.
• Conductors and Insulators: Conductors allow movement of electric charge through them, insulators do not.
• Quantization of Electric Charge: It means that total charge (q) of a body is always an integral multiple of a basic quantum of charge (e)
  q = ne where n = 0, ±1, ±2, ±3$\text{n }=0,\pm \text{1},\pm \text{2},\pm \text{3}$, ….
• Additivity of Electric Charges: Total charge of a system is the algebraic sum of all individual charges in the system.
• Conservation of Electric Charges: The total charge of an isolated system remains uncharged with time.
• Superposition Principle: It is the properties of forces with which two charges attract or repel each other are not affected by the presence of a third (or more) additional charge(s).
• The Electric Field E at a point due to a charge configuration: It is the force on a small positive test charge q placed at the point divided by a magnitude and is given by  |q|4πε0r2$\frac{|q|}{4\pi {\epsilon }_0{r}^2}$
  It is radially outwards from q, if q is positive and radially inwards if q is negative.
  E at a point varies inversely as the square of its distance from q. The plot of E versus r will look like the figure given below: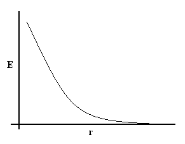
  
• Coulomb’s Law: The mutual electrostatic force between two point charges q1$q_1$ and q2$q_2$ is proportional to the product q1q2$q_1{q}_2$ and inversely proportional to the square of the distance r21$r_{21}$ separating them.
  F→21(force on q2 due to q1)=k(q1q2)r221r ^21${\overrightarrow{F}}_{21}(force\text{ on }{\text{q}}_2\text{ due to }{\text{q}}_1)=\frac{k(q_1{q}_2)}{r_{21}^2}{\hat{r}}_{21}$
  Where r ^21${\hat{r}}_{21}$ is a unit vector in the direction from q1$q_1$ to q2$q_2$ and k =  14πε0$\frac{1}{4\pi {\epsilon }_0}$ is the proportionality constant.
• An Electric Field Line: It is a curve drawn in such a way that the tangent at each point on the curve gives the direction of electric field at that point.
• Important Properties of Field Lines:
  (i) Field lines are continuous curves without any breaks.
  (ii) Two field lines cannot cross each other.
  (iii) Electrostatic field lines start at positive charges and end at negative charges
  (iv) They cannot form closed loops.
• Electric Field at a Point due to Charge q: E→=F→q$\overrightarrow{E}=\frac{\overrightarrow{F}}{q}$
• Electric Field due to an electric dipole in its equatorial plane at a distance r from the centre:E=−p4πε01(a2+r2)32$E=\frac{-p}{4\pi {\epsilon }_0}\frac{1}{{(a^2+r^2)}^{\frac{3}{2}}}$ ≅−p4πε0r3$\cong \frac{-p}{4\pi {\epsilon }_0{r}^3}$ , for r >> a
• Electric Field due to an Electric Dipole on the Axis at a Distance r from the Centre: E=2pr4πε0(r2−a2)2$E=\frac{2pr}{4\pi {\epsilon }_0{(r^2-a^2)}^2}$ ≅2p4πε0r3$\cong \frac{2p}{4\pi {\epsilon }_0{r}^3}$, for r >> a
• A Dipole Placed in Uniform Electric Field E experiences a torque τ⃗ =p⃗ ×E⃗ $\overrightarrow{\tau }=\overrightarrow{p}\times \overrightarrow{E}$ but experience no net force.
• The Electric Flux: ϕ=∫dϕ=∫E→.ds→$\varphi =\int d\varphi =\int \overrightarrow{E}.d\overrightarrow{s}$ is a ‘dot’ product, hence it is scalar.
  Δϕ$\mathrm{\Delta }\varphi$ is positive for all values of θ<π2$\theta <\frac{\pi }{2}$
  Δϕ$\mathrm{\Delta }\varphi$ is negative for all values of θ>π2$\theta >\frac{\pi }{2}$
• Gauss’s Law: The flux of electric field through any closed surface S is 1/ε0 times the total charge enclosed by S.
• Electric field E, due to an infinitely long straight wire of uniform linear charge density λ$\lambda$ :E=λ2πε0r.n∧$E=\frac{\lambda }{2\pi {\epsilon }_{0}r}.\stackrel{\wedge }{n}$
  where r is the perpendicular distance of the point from the wire and nˆ$\hat{n}$ is the radial unit vector in the plane normal to the wire passing through the point.
• Electric field E, due to an infinite thin plane sheet of uniform surface charge density σ: E=σ2ε0.n∧$E=\frac{\sigma }{2{\epsilon }_0}.\stackrel{\wedge }{n}$
  where n∧$\stackrel{\wedge }{n}$ is a unit vector normal to the plane, outward on either side.
• Electric field E, due to thin spherical shell of uniform surface charge density σ: E=q4πεor2rˆ$E=\frac{q}{4\pi {\epsilon }_o{r}^2}\hat{r}$ for r ≥$\ge$ R and E = 0 for r < R where r is the distance of the point from the centre of the shell and R the radius of the shell, q is the total charge of the shell & q = 4πR2σ.
• Electric field outside the charged shell is as though the total charge is concentrated at the centre. The same result is true for a solid sphere of uniform volume charge density.The electric field is zero at all points inside a charged shell.
• Electric field E along the outward normal to the surface is zero and σ is the surface charge density. Charges in a conductor can reside only at its surface. Potential is constant within and on the surface of a conductor. In a cavity within a conductor (with no charges), the electric field is zero.