Electromagnetic Induction-Test Papers

 CBSE Test Paper-01

Class - 12 Physics (Electromagnetic Induction)

---

1. Two coils C1${\mathrm{C}}_1$ , C2${\mathrm{C}}_2$ have N1${\mathrm{N}}_1$ and N2${\mathrm{N}}_2$ turns respectively. Current i1${\mathrm{i}}_1$ in coil C1${\mathrm{C}}_1$ is changing with time. The emf in C2${\mathrm{C}}_2$ is given by

   1. −di1dt$-\frac{d{i}_1}{dt}$
   2. −Mdi1dt$-M\frac{d{i}_1}{dt}$
   3. −Mdi2dt$-M\frac{d{i}_2}{dt}$
   4. −Mdi21dt$-M\frac{d{i}_1^2}{dt}$

2. A pair of adjacent coils has a mutual inductance of 1.5 H. If the current in one coil changes from 0 to 20 A in 0.5 s, change of flux linkage with the other coil is

   1. 45 Wb
   2. 35 Wb
   3. 30 Wb
   4. 40 Wb

3. According to Lenz’s law.

   1. The polarity of induced emf is such that it tends to produce a current which aids the change in magnetic flux that produced it.
   2. The induced emf is proportional rate of change in magnetic flux that produced it.
   3. The polarity of induced emf is such that it tends to produce a current which opposes the change in magnetic flux that produced it.
   4. The induced emf is proportional change in magnetic flux that produced it.

4. The magnetic field between the Horizontal poles of an electromagnet is uniform at any time, but its magnitude is increasing at the rate of 0.020 T/s. The area of a horizontal conducting loop in the magnetic field is 120cm2, and the total circuit resistance, including the meter, is 5Ω$5\mathrm{\Omega }$. Induced emf and the induced current in the circuit are

   1. 0.18 mV, 0.048 mA
   2. 0.20 mV, 0.048 mA
   3. 0.24 mV, 0.048 mA
   4. 0.22 mV, 0.048 mA

5. When current changes from + 2 A to - 2 A in 0.05 sec, an emf of 8 V is induced in a coil. The coefficient of self inductance of the coil is:

   1. 0.8 H
   2. 0.1 H
   3. 0.2 H
   4. 0.4 H

6. A train is moving with uniform velocity from north to south. Will any induced emf appear across the ends of the axle?

7. A metallic piece gets hot when surrounded by a coil carrying high-frequency alternating current. Why?

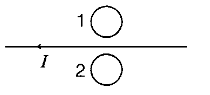
8. Predict the direction of induced current in metal rings 1 and 2 when current I in the wire is steadily decreasing?
   

9. Show that the energy stored in an inductor i.e. the energy required to build current in the circuit from zero to I is 12LI2$\frac{1}{2}L{I}^2$, where L is the self inductance of the circuit.

10. A long solenoid of 20 turns per cm has a small loop of area 4 cm2 placed inside the solenoid normal to its axis. If the current by the solenoid changes steadily from 4 A to 6A in 0.25, what is the (average) induced emf in the loop while the current is changing?

11. A conducting U tube can slide inside another U-tube maintaining electrical contact between the tubes. The magnetic field is perpendicular to the plane of paper and is directed inward. Each tube moves towards the other at constant speed v. Find the magnitude of induced emf across the ends of the tube in terms of magnetic field B, velocity v and width of the tube?
    

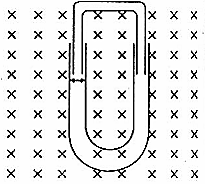
12. 1. A toroidal solenoid with an air core has an average radius of 0.15 m, area of cross section 12×10−4m2$12\times {10}^{-4}{m}^2$ and 1200 turns. Obtain the self inductance of the toroid. Ignore field variation across the cross section of the toroid.
    2. A second coil of 300 turns is wound closely on the toroid above. If the current in the primary coil is increased from zero to 2.0 A in 0.05 s, obtain the induced emf in the secondary coil.

13. A 1.0 m long conducting rod rotates with an angular frequency of 400rad s-1about an axis normal to the rod passing through its one end. The other end of the rod is in contact with a circular metallic ring. A constant magnetic field of 0.5 T parallel to the axis exists everywhere. Calculate the emf developed between the centre and the ring.

14. A rectangular loop of sides 8 cm and 2 cm with a small cut is moving out of a region of uniform magnetic field of magnitude 0.3 tesla directed normal to the loop. What is the voltage developed across the cut if velocity of loop is 1cms−1$1cm{s}^{-1}$ in a direction normal to the (i) longer side (ii) shorter side of the loop? For how long does the induced voltage last in each case?

15. A current of 10 A is flowing in a long straight wire situated near a rectangular coil. The two sides, of the coil, of length 0.2 m are parallel to the wire. One of them is at a distance of 0.05 m and the other is at a distance of 0.10 m from the wire. The wire is in the plane of the coil. Calculate the magnetic flux through the rectangular coil. If the current uniformly to zero in 0.02 s, find the emf induced in the coil and indicate the direction in which the induced current flows.

CBSE Test Paper-01
Class - 12 Physics (Electromagnetic Induction)
Answers

---

1. 2. ​​​​−Mdi1dt$-M\frac{d{i}_1}{dt}$
      Explanation: N2ϕ2∝i1$N_2{\varphi }_2\propto i_1$
      N2ϕ2=Mi1$N_2{\varphi }_2=M{i}_1$
      e2=−N2dϕ2dt=−d(N2ϕ2)dt$e_2=-N_2\frac{d{\varphi }_2}{dt}=-\frac{d(N_2{\varphi }_2)}{dt}$
      e2=−Mdi1dt$e_2=-M\frac{d{i}_1}{dt}$
2. 3. 30 Wb
      Explanation: Δϕ=MΔi=1.5×20=30Wb$\mathrm{\Delta }\varphi =M\mathrm{\Delta }i=1.5\times 20=30\mathrm{W}\mathrm{b}$
3. 3. The polarity of induced emf is such that it tends to produce a current which opposes the change in magnetic flux that produced it.
      Explanation: The direction of an induced emf, or the current, in any circuit is such as to oppose the cause that produces it.
      If the direction of the induced current were such as not to oppose then we would be obtaining electrical energy continuously without doing work, which is impossible.
4. 3. 0.24 mV, 0.048 mA
      Explanation: e = Rate of change of magnetic field ×$\times$ area
      =0.02×120×10−4=0.24mV$=0.02\times 120\times {10}^{-4}=0.24\mathrm{m}\mathrm{V}$
      i=eR=0.245=0.48mA$i=\frac{e}{R}=\frac{0.24}{5}=0.48\mathrm{m}\mathrm{A}$
5. 2. 0.1 H
      Explanation: L=−eΔiΔt$L=-\frac{e}{\frac{\mathrm{\Delta }i}{\mathrm{\Delta }t}}$
      ΔiΔt=−40.05=−80$\frac{\mathrm{\Delta }i}{\mathrm{\Delta }t}=-\frac{4}{0.05}=-80$
      e = 8 volt
      L=−8−80=0.1H$\mathrm{L}=-\frac{8}{-80}=0.1\mathrm{H}$

6. Yes. The vertical component of earth's magnetic field shall induce emf.

7. It happens due to production of eddy currents.

8. According to Lenz's law the induced current in:

   1. ring 1 is clockwise.
   2. ring 2 is anti-clockwise.

9. Energy spent by the source to increase current from i to i + di in time dt in an inductor.
   =Ldidt×i×dt$=L\frac{di}{dt}\times i\times dt$
   = Li di
   Energy required to increase current from 0 to I
   E=∫0ILidi=L[i22]I0$E=\underset{0}{\overset{I}{\int }}Lidi=L{\left[\frac{i^2}{2}\right]}_0^I$
   E=L[I22−0]=12LI2$E=L\left[\frac{I^2}{2}-0\right]=\frac{1}{2}L{I}^2$

10. The induced emf,
    ε=−dϕdt$\epsilon =-\frac{d\varphi }{dt}$
    ε=ddt(BAcosϕ)(∵cosϕ=1)$\epsilon =\frac{d}{dt}(BA\cos \varphi )(\because \cos \varphi =1)$
    =20×100×4×10−40.2$=\frac{20\times 100\times 4\times {10}^{-4}}{0.2}$ = 4 volt.

11. Relative velocity of the tube of width l = v - (-v) = 2v
    ∴$\therefore$ induced emf,
    ε$\epsilon$= Bl(2v)
    = 2 Blv

12. 1. B=μ0n1I=μ0N1I1=μ0N1I2πr$B={\mu }_0{n}_{1}I=\frac{{\mu }_0{N}_{1}I}{1}=\frac{{\mu }_0{N}_{1}I}{2\pi r}$
       Total magnetic flux, ϕB=N1BA=μ0N21IA2πr${\varphi }_B=N_{1}BA=\frac{{\mu }_0{N}_1^{2}IA}{2\pi r}$
       But ϕB=LI${\varphi }_B=LI$
       ∴L=μ0N21A2πr$\therefore L=\frac{{\mu }_0{N}_1^{2}A}{2\pi r}$
       Or L=4π×10−7×1200×1200×12×10−42π×0.15H$L=\frac{4\pi \times {10}^{-7}\times 1200\times 1200\times 12\times {10}^{-4}}{2\pi \times 0.15}H$
       =2.3×10−3H$=2.3\times {10}^{-3}H$= 2.3 mH
    2. |E|=ddt(ϕ2)$\left|E\right|=\frac{d}{dt}({\varphi }_2)$ where ϕ2${\varphi }_2$ is the total magnetic flux linked with the second coil.
       |E|=ddt(N2BA)=ddt[N2μ0N1I2πrA]$\left|E\right|=\frac{d}{dt}(N_{2}BA)=\frac{d}{dt}\left[N_2\frac{{\mu }_0{N}_{1}I}{2\pi r}A\right]$
       or |E|=μ0N1N2A2πrdIdt$\left|E\right|=\frac{{\mu }_0{N}_1{N}_{2}A}{2\pi r}\frac{dI}{dt}$
       |E|=4π×10−7×1200×300×12×10−4×22π×0.15×0.05V$\left|E\right|=\frac{4\pi \times {10}^{-7}\times 1200\times 300\times 12\times {10}^{-4}\times 2}{2\pi \times 0.15\times 0.05}V$ = 0.023 V

13. Here, l = 1 m, ω=400s−1$\omega =400s^{-1}$ B = 0.5 T, e = ?
    Note that linear velocity of one end of rod is zero and linear velocity of other end is (1ω)$\left(1\omega \right)$. Average linear velocity
    v=0+1ω2=1ω2(∵v=rω)$v=\frac{0+1\omega }{2}=\frac{1\omega }{2}\left(\because v=r\omega \right)$
    ∴e=Blv=Bl(1ω)2=Bl2ω2=0.5×12×4002=100v$\therefore e=Blv=Bl\frac{\left(1\omega \right)}{2}=\frac{B{l}^2\omega }{2}=\frac{0.5\times 1^2\times 400}{2}=100v$

14. Given,
    Length of loop, l = 8 cm =8×10−2m$=8\times {10}^{-2}m$
    Breadth of loop, b = 2 cm=2×10−2m$=2\times {10}^{-2}m$
    Strength of magnetic field,
    B = 0.3 T
    Velocity of loop v = 1 cm / sec=10−2m/sec$={10}^{-2}m/sec$
    Let the field be perpendicular to the plane of the paper directed inwards.

    1. The magnitude of induced emf,
       ε=B.l.v$\epsilon =B.l.v$
       =0.3×8×10−2×10−2$=0.3\times 8\times {10}^{-2}\times {10}^{-2}$
       =2.4×10−4V$=2.4\times {10}^{-4}V$
       Time for which induced emf will last is equal to the time taken by the coil to move outside the field is
       I=distancetravelledvelocity=2×10−210−2m$I=\frac{dis\tan cetravelled}{velocity}=\frac{2\times {10}^{-2}}{{10}^{-2}}m$ = 2 sec.
    2. The conductor is moving outside the field normal to the shorter side.
       b=2×10−2m$b=2\times {10}^{-2}m$
       The magnitude of induced emf is
       ε=B.b.v$\epsilon =B.b.v$
       =0.3×2×10−2×10−2$=0.3\times 2\times {10}^{-2}\times {10}^{-2}$
       =0.6×10−4V$=0.6\times {10}^{-4}V$
       Time, t=distancetravelledvelocity=8×10−210−2sec=8sec$t=\frac{dis\tan cetravelled}{velocity}=\frac{8\times {10}^{-2}}{{10}^{-2}}sec=8sec$

15. Consider a strip of width dr at a distance r from the straight wire.
    Magnetic field at the location of the strip due to the wire,
    B=μ0I2πr$B=\frac{{\mu }_{0}I}{2\pi r}$z
    Area of strip, dA = ldr
    Magnetic flux linked with the strip,
    dϕB=BdA=μI2πrldr$d{\varphi }_B=BdA=\frac{\mu I}{2\pi r}ldr$
    Total magnetic flux linked with the coil,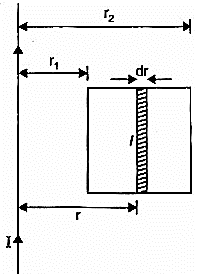
    
    dϕB=μ0Il2πdrr$d{\varphi }_B=\frac{{\mu }_{0}Il}{2\pi }\frac{dr}{r}$
    ∫dQB=μ0Il2π∫r1r2dlr$\int d{Q}_B=\frac{{\mu }_{0}Il}{2\pi }\underset{r_1}{\overset{r_2}{\int }}\frac{dl}{r}$
    QB=μ0Il2π[loger2−loger1]$Q_B=\frac{{\mu }_{0}Il}{2\pi }[{\log }_e{r}_2-{\log }_e{r}_1]$
    QB=μ0I⋅12π[loger]r2r1$Q_B=\frac{{\mu }_{0}I\cdot 1}{2\pi }{\left[{\log }_{e}r\right]}_{r1}^{r2}$
    QB=μ0Il2πloger2r1$Q_B=\frac{{\mu }_{0}Il}{2\pi }lo{g}_e\frac{r_2}{r_1}$
    ϕB=4π×10−7×10×0.22πlog[0.100.05]${\varphi }_B=\frac{4\pi \times {10}^{-7}\times 10\times 0.2}{2\pi }log[\frac{0.10}{0.05}]$
    =4×10−7loge2$=4\times {10}^{-7}lo{g}_{e}2$
    =4×0.693×10−7Wb$=4\times 0.693\times {10}^{-7}Wb$
    2.77×10−7Wb$2.77\times {10}^{-7}Wb$
    Induced emf
    |E|=−dϕBdt=2.77×10−70.02V$\left|E\right|=-\frac{d{\varphi }_B}{dt}=\frac{2.77\times {10}^{-7}}{0.02}V$
    =1.39×10−5V$=1.39\times {10}^{-5}V$
    Magnetic field, due to wire, at the location of the coil is perpendicular to the plane of the coil and directed inwards. When current is reduced to zero, this magnetic field decreases. To oppose this decrease, induced current shall flow clockwise, so that its magnetic field is also perpendicular to the plane of the coil and downward.