Electrostatic Potential and Capacitance-Test Papers

 CBSE Test Paper-01

Class - 12 Physics (Electrostatics Potential and Capacitance)

---

1. Correct formula for capacitance in terms of area A and distance d, of a parallel plate capacitor in vacuum is

   1. ϵ0Ad2${ϵ}_0\frac{A}{d^2}$
   2. ϵ0A2d${ϵ}_0\frac{A^2}{d}$
   3. ϵ0dA${ϵ}_0\frac{d}{A}$
   4. ϵ0Ad${ϵ}_0\frac{A}{d}$
2. Two parallel plate capacitors of capacitances C and 2C are connected in parallel and charged to a potential difference V by a battery. The battery is then disconnected and the space between the plates of capacitor C is completely filled with a material of dielectric constant K = 3. The potential difference across the capacitors now becomes

   1. 2V5$\frac{2V}{5}$
   2. 3V6$\frac{3V}{6}$
   3. V4$\frac{V}{4}$
   4. 3V5$\frac{3V}{5}$
3. A variable capacitor and an electroscope are connected in parallel to a battery. The reading of the electroscope would be decreased by
   1. Decreasing the battery potential
   2. Increasing the area of overlapping of the plates
   3. Decreasing the distance between the plates
   4. Placing a dielectric between the plates
4. The capacity of a pure capacitor is 1 farad. In DC circuit its effective resistance will be
   1. infinite
   2. zero
   3. 1 Ω$\mathrm{\Omega }$
   4. 2 ohm
5. In circuits, a difference in potential from one point to another is often called
   1. volts
   2. AT
   3. field
   4. voltage

6. What is the geometrical shape of equipotential surfaces due to a single isolated charge?

7. Draw equipotential surfaces due to a single point charge.

8. Two charges 2 µC and -2 µC are placed at points A and B, 5 cm apart. Depict an equipotential surface of the system.

9. What are the dimensions of capacitance?

10. A slab of material of dielectric constant K has the same area as that of the plates of a parallel plate capacitor, but has the thickness d/2, where d is the separation between the plates. Find out the expression for its capacitance when the slab is inserted between the plates of the capacitor.

11. Two capacitors of 1 µF capacitance are connected to a battery of 6 V. Initially switch S is closed. After sometime S is left open and dielectric slab of dielectric constant K = 3 are inserted to fill completely the space between the plates of the two capacitors.
    How will the (i) charge and (ii) potential difference between the plates of the capacitors be affected after the slabs are inserted?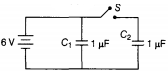
    

12. Electric charge is distributed uniformly on the surface of a spherical rubber balloon. Show how the value of electric intensity and potential vary

    1. on the surface,
    2. inside and
    3. outside?

13. A 5μF$5\mu F$ capacitor is charged by a 100 V supply. The supply is then disconnected and the charged capacitor is connected to another uncharged 3μF$3\mu F$ capacitor. How much electrostatic energy of the first capacitor is lost in the process of attaining the steady situation?

14. 1. Derive the expression for the capacitance of a parallel plate capacitor having plate area A and plate separation d.
    2. Two charged spherical conductors of radii R1 and R2 when connected by a conducting plate respectively. Find the ratio of their surface charge densities in terms of their radii.
15. 1. Explain using suitable diagrams, the difference in the behaviour of a
       1. conductor and
       2. dielectric in the presence of external electric field. Define the terms polarisation of a dielectric and write its relation with susceptibility.
    2. A thin metallic spherical shell of radius R carries a charge Q on its surface. A point charge Q/2 is placed at its centre C and another charge + 2Q is placed outside the shell at a distance x from the centre as shown in the figure. Find
       
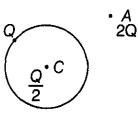
       1. the force on the charge at the centre of shell and at the point A,
       2. the electric flux through the shell.

CBSE Test Paper-01
Class - 12 Physics (Electrostatics Potential and Capacitance)
Answers

---

1. 4. ϵ0Ad${ϵ}_0\frac{A}{d}$

      Explanation: The capacitance of a parallel plate capacitor is given by C=ε0Ad$C=\frac{{\epsilon }_{0}A}{d}$

2. 4. 3V5$\frac{3V}{5}$

      Explanation: The charges on the capacitors after being charged to a potential V are Q1 = CV; Q2 = 2CV.
      After being filled with a material of dielectric K = 3 the capacitor which initially had a capacitance C has now the capacitance KC = 3C. The common potential
      V1=Total chargeTotal capacitance=Q1+Q23C+2C$V_1=\frac{\text{Total charge}}{\text{Total capacitance}}=\frac{Q_1+Q_2}{3C+2C}$
      =CV+2CV5C=35V$=\frac{CV+2CV}{5C}=\frac{3}{5}V$

3. 1. Decreasing the battery potential
      Explanation: An electroscope is a device which measures the potential difference. If it is connected in parallel to the capacitor, the potential across it will be equal to the potential across the capacitor, which is equal to the potential across the battery. On decreasing the battery potential, the potential difference across the electroscope reduces and hence the reading reduces. While the capacitor is connected to the battery, Placing a dielectric between the plates, or decreasing the distance between the plates or increasing the area of the plates will not change the potential difference across it; since it will always remain equal to the potential difference maintained by the battery. In the cases B, C and D, The capacitance of the capacitor, however increases; but this increase happens due to increase in the charge stored in the capacitor while the potential remains constant.
4. 1. infinite
      Explanation: Capacitor does not allow DC to pass through it. The effective capacitance or the capacitive reactance XC=1Cω$X_C=\frac{1}{C\omega }$,
      where ω is the frequency of voltage source.
      Since DC current is a constant current, its frequency is zero.
      The capacitive reactance is therefore infinity.
5. 4. voltage
      Explanation: Voltage is an electrical potential difference, the difference in electric potential between two places. The unit for electrical potential difference, or voltage, is the volt.

6. The equipotential surfaces produced by a single point charge are spherically symmetrical surfaces which are concentric.
   In concentric spheres which are as shown below in the figure, the lines of force point radially outwards, so they are perpendicular to the equipotential surfaces at all points.
   If we place another unit positive charge at any point on these surfaces, that will repelled along the the direction of the electric field intensity i.e. radially outwards to the surfaces.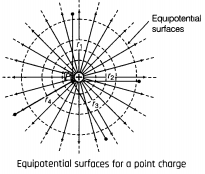
   

7. Equipotential surfaces due to a single point charge are concentric sphere having charge at the centre. Electric field lines are always normally outwards from the spherical surfaces.
   

8. Given, qA=2μC=2×10−6C$q_A=2\mu C=2\times {10}^{-6}C$
   qg=−2μC=−2×10−6C$q_g=-2\mu C=-2\times {10}^{-6}C$ and r = 5 cm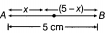
   
   As, potential at point O is zero.
   V=2×10−64πε0x×10−2+−2×10−64πε0(5−x)×10−2=0$V=\frac{2\times {10}^{-6}}{4\pi {\epsilon }_{0}x\times {10}^{-2}}+\frac{-2\times {10}^{-6}}{4\pi {\epsilon }_0(5-x)\times {10}^{-2}}=0$
   or 2×10−64πε0x×10−2=2×10−64πε0(5−x)×10−2$\frac{2\times {10}^{-6}}{4\pi {\epsilon }_{0}x\times {10}^{-2}}=\frac{2\times {10}^{-6}}{4\pi {\epsilon }_0(5-x)\times {10}^{-2}}$
   or x = 5 - x ⇒$\Rightarrow$ x = 2.5 cm
   Hence equipotential surface is a plane normal to the axis of the dipole and lies at the mid point of the axis.

9. [M−1L−2A2T4]$\left[M^{-1}{L}^{-2}{A}^2{T}^4\right]$

10. Initially, when there is vacuum between the two plates of the capacitor, then capacitance of the capacitor becomes C0=ε0Ad$C_0=\frac{{\epsilon }_{0}A}{d}$,
    where, A is the area of each plate of the capacitor.
    Suppose that the capacitor is connected to a battery, an electric field E0 is produced.
    Now, if we insert the dielectric slab of dielectric constant K and of thickness t = d/2, the electric field reduces to E = E0/K.
    Now, the gap between plates is divided in two parts, for distance t, there is electric field E and for the remaining distance (d - t) the electric field is E0.
    If V be the potential difference between the plates of the capacitor after inserting the dielectric slab, then V = Et + E0(d - t)
    ⇒V=Ed2+E0d2=d2(E+E0)[∵t=d2]$\Rightarrow V=\frac{Ed}{2}+\frac{E_{0}d}{2}=\frac{d}{2}\left(E+E_0\right)\left[\because t=\frac{d}{2}\right]$
    ⇒V=d2(E0K+E0)$\Rightarrow V=\frac{d}{2}\left(\frac{E_0}{K}+E_0\right)$
    =dE02K(K+1)$=\frac{d{E}_0}{2K}(K+1)$ [ As, E0E=K]$\left[\text{ As, }\frac{E_0}{E}=K\right]$
    Now, E0=σε0=qε0A$E_0=\frac{\sigma }{{\epsilon }_0}=\frac{q}{{\epsilon }_{0}A}$, Hence the potential becomes V=d2K⋅qε0A(K+1)$V=\frac{d}{2K}\cdot \frac{q}{{\epsilon }_{0}A}(K+1)$
    Again we know that, C=qV=2Kε0Ad(K+1)$C=\frac{q}{V}=\frac{2K{\epsilon }_{0}A}{d(K+1)}$(substituting the value of V)

11. 1. According to the diagram, when the switch S is closed, the two capacitors C1 and C2 in parallel will be charged by the same potential difference V.
       
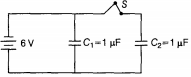
       So, charge on capacitor C1

       q1=C1V=1×6=6μC$q_1=C_{1}V=1\times 6=6\mu \mathrm{C}$ ....(i)
       and charge on capacitor C2
       q2=C2V=1×6=6μC$q_2=C_{2}V=1\times 6=6\mu C$ ...(ii)
       Hence total charge, q = q1 + q2 = 6 + 6 = 12µC (before the switch S is closed) Now when S is left open, there will be no change in the stored charge value of C2 and the change in charge value in C1 is given in the answer (ii).

    2. When switch S is opened and dielectric is introduced. Then
       
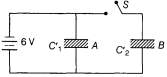
       Capacity of both the capacitors becomes K times
       i.e. C′1=C′2=KC=3×1=3μF(asC′1=C′2)$C_1^{\prime }=C_2^{\mathrm{\prime }}=KC=3\times 1=3\mu F\left(\mathrm{as}{C}_1^{\mathrm{\prime }}=C_2^{\prime }\right)$
       Capacitor A remains connected to battery
       ∴V′1=V=6V$\therefore V_1^{\mathrm{\prime }}=V=6\mathrm{V}$
       q′1=Kq1=3×6μC=18μC$q_1^{\mathrm{\prime }}=K{q}_1=3\times 6\mu C=18\mu C$ (charge in C1 is increased to 3 times of the previous value)
       Capacitor B becomes isolated, charge in it will remain same
       ∴q′2=q2 ⇒ C′2V′2=C2V2$\therefore q_2^{\prime }=q_2\Rightarrow C_2^{\prime }{V}_2^{\prime }=C_2{V}_2$ or (KC)V′2=CV$(KC)V_2^{\prime }=CV$ (C2 = C, C'2 = KC)
       or V2=(VK)=63=2V$V_2=\left(\frac{V}{K}\right)=\frac{6}{3}=2V$ (potential difference of the capacitor B is reduced to a factor of 3)

12. On the surface E = constant, V = constant. Inside the surface, E = 0, V = constant = potential on surface. Outside the balloon.
    E∝1r2$E\propto \frac{1}{r^2}$ and V∝1r$V\propto \frac{1}{r}$
    where r is the distance of the point from the centre of the balloon.

13. Initial energy stored in 5μF$5\mu F$ capacitor,
    Ui=12CV2=12×5×10−6×(100)2$U_i=\frac{1}{2}C{V}^2=\frac{1}{2}\times 5\times {10}^{-6}\times (100{)}^2$
    =2.5×10−2J$=2.5\times {10}^{-2}J$
    Charge on 5 mF capacitor =5×10−6×100$=5\times {10}^{-6}\times 100$
    =5×10−4C[∵q=CV]$=5\times {10}^{-4}C\left[\because q=CV\right]$
    The two capacitors attain a common potential V when they are connected together.
    V=Totalchargetotalcapacitor=5×10−4(5+3)×10−6=1252V$V=\frac{Totalch\arg e}{totalcapacitor}=\frac{5\times {10}^{-4}}{(5+3)\times {10}^{-6}}=\frac{125}{2}V$
    Final energy of the combination,
    Uf=12×(5+3)×10−6×(1252)2=1.56×10−2J$U_f=\frac{1}{2}\times (5+3)\times {10}^{-6}\times {\left(\frac{125}{2}\right)}^2=1.56\times {10}^{-2}J$
    Electrostatic energy lost in the process of attaining the steady state
    =Ui−Uf=(2.5−1.56)×10−2$=U_i-U_f=(2.5-1.56)\times {10}^{-2}$
    =0.94×10−2J$=0.94\times {10}^{-2}J$

14. 1. Parallel plate capacitor consists of two thin conducting plates each of area A held parallel to each other at a suitable distance d. One of the plates is insulated and other is earthed. Say, there is vacuum or air between the plates. Structure of a parallel plate capacitor is shown below.
       
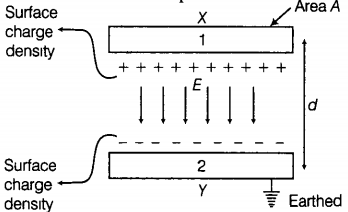
       Suppose, the plate X is given a charge of +q coulomb. By induction, -q coulomb of charge is produced on the inner surface of the plate Y and +q coulomb on the outer surface. Since, the plate Y is connected to the earth, hence the relatively weak charge +q residing far away i.e. on the outer surface flows to the earth. Thus, the plates X and Y have equal and opposite charges +q and -q respectively
       Suppose, the surface density of charge on each plate is σ$\sigma$, We know that the intensity of electric field at a point between two plane parallel sheets of equal and opposite charges is = σ2ϵ0−(−σ2ϵ0)=$\frac{\sigma }{2{ϵ}_0}-(-\frac{\sigma }{2{ϵ}_0})=$ σ/ε0$\sigma /{\epsilon }_0$ [+σ2ϵ0 and −σ2ϵ0$\frac{+\sigma }{2{ϵ}_0}and\frac{-\sigma }{2{ϵ}_0}$ are electric field intensities in between the two plates due to charges +q and -q on the two plates of the capacitor respectively], where ε0${\epsilon }_0$ is the permittivity of free space. The intensity of electric field between the plates will be given by, E=σε0$E=\frac{\sigma }{{\epsilon }_0}$
       The charge on each plate is q and the area of each plate is A. Thus,
       σ=qA and E=qε0A$\sigma =\frac{q}{A}\text{ and }E=\frac{q}{{\epsilon }_{0}A}$............(i)
       Now, let the potential difference between the two plates be V volt. Then, the electric field between the plates is given by
       E=Vd or V=Ed$E=\frac{V}{d}\text{ or }V=Ed$.....(ii)
       Substituting the value of E from equation (i) into equation (ii), we get
       V=qdε0A$V=\frac{qd}{{\epsilon }_{0}A}$
       Now capacitance of the parallel plate capacitor is
       C=qV=qqd/ε0A or C=ε0Ad$C=\frac{q}{V}=\frac{q}{qd/{\epsilon }_{0}A}\text{ or }C=\frac{{\epsilon }_{0}A}{d}$
       Where, ε0=8.85×10−12C2−Nm−2${\epsilon }_0=8.85\times {10}^{-12}{\mathrm{C}}^2-{\mathrm{N}\mathrm{m}}^{-2}$ is the permittivity of vacuum or air.
    2. Surface charge density of a spherically charged body is given by
       σ=q4πR2$\sigma =\frac{q}{4\pi R^2}$
       After connecting both the conductors, their potentials will become equal.
       ⇒Kq1Rl=Kq2R2$\Rightarrow \frac{K{q}_1}{R_{\mathrm{l}}}=\frac{K{q}_2}{R_2}$ [ For a spherically charged conductor with charge q potential is given by, V=14πε0qR or V=KqR$V=\frac{1}{4\pi {\epsilon }_0}\frac{q}{R}\text{ or }V=\frac{Kq}{R}$]
       ∴q1q2=R1R2 Hence σ1σ2=q1/4πR21q2/4πR22$\therefore \frac{q_1}{q_2}=\frac{R_1}{R_2}Hence\frac{{\sigma }_1}{{\sigma }_2}=\frac{q_1/4\pi R_1^2}{q_2/4\pi R_2^2}$
       =q1q2(R2R1)2=R1R2×(R2R1)2=R2R1$=\frac{q_1}{q_2}{\left(\frac{R_2}{R_1}\right)}^2=\frac{R_1}{R_2}\times {\left(\frac{R_2}{R_1}\right)}^2=\frac{R_2}{R_1}$
1. 1. When a conductor is placed in an external electric field, the free charges present inside the conductor redistribute themselves in such a manner that the electric field due to induced charges opposes the external field within the conductor. This happens until a static situation is achieved, i.e. when the two fields cancels each other, then the net electrostatic field in the conductor becomes zero.
   2. Dielectrics are non-conducting substances. i.e. they have no charge carriers. Thus, in a dielectric, free movement of charges is not possible. When a dielectric is placed in an external electric field, the molecules are re-oriented and thus induces a net dipole moment in the dielectric. This produces an electric field. The diagram clearly shows that the net electric field in case of a conductor becomes zero, whereas in case of a dielectric net electric field intensity becomes non zero.
      
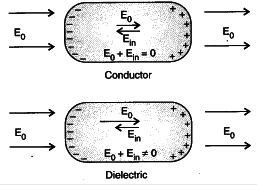
      However, the opposing field is so induced that does not exactly cancel the external field. It only reduces it. And the resultant electric field reduces by some value.
      Both polar and non-polar dielectric develop net dipole moment in the presence of an external field. The dipole moment per unit volume of the substance is called polarisation and is denoted by P for linear isotropic dielectrics. P=χE$P=\chi E$, χ$\chi$ is the susceptibility.
1. At point C, inside the shell. The electric field inside a spherical shell is zero. Thus, the force experienced by the charge Q/2 kept at the centre C of the shell will also be zero.
   ∵FC=qE(E nside the shell =0$\because F_C=qE(E_{\text{ nside the shell }}=0$)
   ∴FC=0$\therefore F_C=0$
   At point 'A', magnitude of the force experienced by charge +2Q there, IFA= 2Q × (14πε03Q/2x2)$\left(\frac{1}{4\pi {\epsilon }_0}\frac{3Q/2}{x^2}\right)$ (since 3Q/2 is the net charge of the shell)
   ∴F=3Q24πε0x2$\therefore F=\frac{3Q^2}{4\pi {\epsilon }_0{x}^2}$ , direction of this force is away from shell
2. Electric flux through the shell, ϕ=1ε0$\varphi =\frac{1}{{\epsilon }_0}$ × magnitude of the net charge enclosed by the shell. (In this case there is no effect of the charge which lies above the shell)
   ⇒ϕ=1/ε0×Q/2=Q/2ε0

CBSE Test Paper-04
Class - 12 Physics (Electrostatic Potential and Capacitance)

---

1. The dielectric constant K of an insulator will be-

   1. 0.4
   2. 4
   3. -4
   4. 0
2. If a charge q0${\mathrm{q}}_0$ is there in a electric field caused by several point charges qi${\mathrm{q}}_i$ The potential energy of q0${\mathrm{q}}_0$ is given by

   1. 14πϵ0Σqiq0r2$\frac{1}{4\pi {ϵ}_0}\mathrm{\Sigma }\frac{q_i{q}_0}{r^2}$
   2. 14πϵ0Σqiq0r$\frac{1}{4\pi {ϵ}_0}\mathrm{\Sigma }\frac{q_i{q}_0}{r}$
   3. 14πϵ0Σqiq0r3$\frac{1}{4\pi {ϵ}_0}\mathrm{\Sigma }\frac{q_i{q}_0}{r^3}$
   4. 12πϵ0Σqiq0r$\frac{1}{2\pi {ϵ}_0}\mathrm{\Sigma }\frac{q_i{q}_0}{r}$
3. For a parallel plate capacitor and a dielectric of dielectric constant K When a dielectric material is inserted between the plates while ____________ the potential difference between the plates decreases by a factor K

   1. the charge varies continously
   2. the charge is increased,
   3. the charge is decreased,
   4. the charge is kept constant,
4. An electrolytic capacitor is marked 8 μF$\mu \mathrm{F}$, 220 V. It can be used in a circuit where the p.d. across the capacitor may be

   1. 200 V
   2. 300 V
   3. 1000 V
   4. 500 V
5. Electric-field magnitude E at points inside and outside a positively charged spherical conductor having charge Q and a radius R are

   1. 0, 14πϵ0QR$\frac{1}{4\pi {ϵ}_0}\frac{Q}{R}$
   2. 14πϵ0QR2$\frac{1}{4\pi {ϵ}_0}\frac{Q}{R^2}$
   3. less than 0,14π∈0$\frac{1}{4\pi \in 0}$qr2$\frac{q}{r^2}$ where r>R
   4. greater than 0,14πϵ0QR2$\frac{1}{4\pi {ϵ}_0}\frac{Q}{R^2}$

6. What is the work done in moving a test charge q through a distance of 1 cm along the equatorials axis of an electric dipole?

7. The figure shows the field lines of a positive charge. Is the work done by the field in moving a small positive charge from Q to P positive or negative?
   

8. A charge q is moved from a point A above a dipole of dipole moment p to a point B below the dipole in equatorial plane without acceleration. Find the work done in this process.
   

9. The discharging current in the atmosphere due to the small conductivity of air is known to be 1800 A on an average over the globe. Why then does the atmosphere not discharge itself completely in due course and become electrically neutral? In other words, what keeps the atmosphere charged?

10. Guess a possible reason why water has a much greater dielectric constant (=80) than say, mica (=6).

11. A parallel plate capacitor with air between the plates has a capacitance of 8 pF (1 pF = 10-12F). What will be the capacitance if the distance between the plates is reduced by half, and the space between them is filled with a substance of dielectric constant 6?

12. What is an equipotential surface?A uniform electric field E→$\overrightarrow{E}$of 300NC−1$300N{C}^{-1}$ is directed along PQ. A, B and C are three points in the field having x and y coordinates (in metres) as shown in the figure, calculate potential difference between the points.(i) A and B (ii) B and C

13. Two charges 2μC$2\mu C$ and −2μC$-2\mu C$ are placed at points A and B, 6 cm apart.

    1. Identify an equipotential surface of the system.
    2. What is the direction of electric field at every point on this surface?
14. 1. Write two characteristics of equipotential surfaces.
    2. Draw the equipotential surfaces due to an electric dipole.

15. Two charged conducting spheres of radii a and b are connected to each other by a wire. What is the ratio of electric fields at the surfaces of the two spheres? Use the result obtained to explain why charge density on the sharp and pointed ends of a conductor is higher than on its flatter portions.

CBSE Test Paper-04
Class - 12 Physics (Electrostatic Potential and Capacitance)
Answers

---

1. 2. 4
      Explanation: Dielectric constant of air is 1. All dielectrics generally have a value of the dielectric constant greater than 1.
      K=FFm$K=\frac{F}{F_m}$
      where Fm is the force between two charged particles in a medium of dielectric constant K and F is the force between the two charges when placed in air.The force between two charges is greatest in air or vacuum and it decreases when any medium is placed between the charges. K cannot have negative, fractional or zero values.
2. 2. 14πϵ0Σqiq0r$\frac{1}{4\pi {ϵ}_0}\mathrm{\Sigma }\frac{q_i{q}_0}{r}$

      Explanation: Potential energy of charge q0 placed at a distance r1 in a field created by a single charge q1 is 

      ℧1=q1q04πε0r1${\mho }_1=\frac{q_1{q}_0}{4\pi {\epsilon }_0{r}_1}$
      In a field created by multiple charges q1, q2,q3,…qi the potential energy of the charge q0 is the scaler sum of potential energies due to each of the charges q1, q2, q3,…qi. As electrostatic potential energy is a scaler quantity. Thus
      The total potential energy of the charge q0 is ℧=∑1iqiq04πε0ri$\mho =\sum _1^i\frac{q_i{q}_0}{4\pi {\epsilon }_0{r}_i}$
3. 4. the charge is kept constant,
      Explanation: When a dielectric material is introduced in between the plates of a charged capacitor, which is disconnected from the battery, the charge remains constant, while the potential decreases by a factor K. The charge on the plates will increase if the dielectric material is slipped in between the plates of a capacitor which remain connected to the battery. In this case, the potential across the plates of the capacitor remains constant being equal to the battery voltage.
4. 1. 200 V
      Explanation: The break down potential of the capacitor is 220 V. In order to prevent damage to a capacitor, it should be always used in a circuit where the p.d is less than its break down potential. The p.d difference can only be 200 V.
5. 3. less than 0, 14π∈0$\frac{1}{4\pi \in 0}$, qr2$\frac{q}{r^2}$ where r>R
      Explanation: As in a conductor charge always reside on surface thus inside the conductor field will be zero. At outside the sphere field will be just as due to a point charge.
6. As Veq=0$V_{eq}=0$
   Work done in moving a positive test charge q through a distance 1 cm is:
   W=qV=q×0=0$W=qV=q\times 0=0$

7. Negative; As the charge is displaced against the force exerted by the field.

8. Electrostatic potential, V ∝$\propto$ charge/distance. Now here both A and B point are at same distances (say r) from both the charges. So potential at the two points, VA = VB = (+qr+−qr=0$\frac{+q}{r}+\frac{-q}{r}=0$). Hence work done =q(VA - VB) = 0.

9. Thunderstorms and ground lightning all over the globe charge the atmosphere continually and discharged through regions of ordinary weather. The two opposing currents are, on an average in equilibrium.

10. Water has a much greater dielectric constant than mica because of the high degree of association of water molecules each of which has a permanent dipole moment of about 0.6×10−29cm$0.6\times {10}^{-29}cm$.

11. C0=ε0Ad$C_0=\frac{{\epsilon }_{0}A}{d}$ or ε0Ad=8×10−12$\frac{{\epsilon }_{0}A}{d}=8\times {10}^{-12}$
    If the distance is reduced to half i.e. d/2 and space between the plates is filled by a substance of k = 6.
    C = kC0
    Then, C=kε0⋅Ad/2$C=\frac{k{\epsilon }_0\cdot A}{d/2}$
    =2k(ε0A)d$=\frac{2k({\epsilon }_{0}A)}{d}$
    =2×6×8×10−12$=2\times 6\times 8\times {10}^{-12}$
    =96×10−12F$=96\times {10}^{-12}F$
    or C = 96 pF

12. Equipotential surface is defined as a surface that has same electric potential at its every point.
    1. No work is done in taking a + ve charge from A to B because the charge moves perpendicular to the electric field.
       ∴$\therefore$ Potential difference between A and B = 0
    2. Since E=−ΔVΔx$E=-\frac{\mathrm{\Delta }V}{\mathrm{\Delta }x}$
       Potential difference between B and C
       ΔV=−EΔx$\mathrm{\Delta }V=-E\mathrm{\Delta }x$
       =−300×7=−2100V$=-300\times 7=-2100V$
13. Given, q1=2μC=2×10−6C$q1=2\mu C=2\times {10}^{-6}C$q2=−2μC=−2×10−6C$q_2=-2\mu C=-2\times {10}^{-6}C$
    1. Potential will be zero due to both charges at equipotential surface
       
       14πε0[q1x+q2(0.06−x)]=0$\frac{1}{4\pi {\epsilon }_0}\left[\frac{q_1}{x}+\frac{q_2}{(0.06-x)}\right]=0$
       or q1x=−q2(0.06−x)$\frac{q_1}{x}=-\frac{q_2}{(0.06-x)}$
       or 2×10−6x=(−2×10−6)[(0.06)−x]$\frac{2\times {10}^{-6}}{x}=\frac{(-2\times {10}^{-6})}{\left[(0.06)-x\right]}$
       or x = 0.06 - x
       x=0.062=0.03m$x=\frac{0.06}{2}=0.03m$
       i.e. the plane normal to AB and passing through its mid point has zero potential everywhere.
    2. The direction of electric field is normal to the plane in the AB direction.
14. 1. 1. Two equipotential surfaces do not intersect each other as normals at the point of intersection on two surfaces will give two different directions of same electric field which is impossible.
       2. Closely spaced equipotential surfaces represent strong electric field and vice-versa.
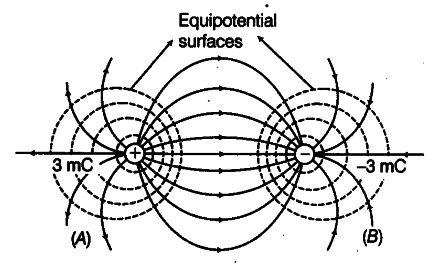
    2. Equipotential surfaces of an electric dipole having charges +3 mC and -3 mC are shown below
       

15. Suppose that two connected conducting spheres of radii a and b possess charges q1and q2respectively. On the surface of the two spheres, the potential will be
    V1=14πε0⋅q1a$V_1=\frac{1}{4\pi {\epsilon }_0}\cdot \frac{q_1}{a}$
    V2=14πε0⋅q2b$V_2=\frac{1}{4\pi {\epsilon }_0}\cdot \frac{q_2}{b}$
    Till the potentials of two conductors become equal the flow of charges continue.
    V1 = V2
    or 14πε0⋅q1a=14πε0⋅q2b$\frac{1}{4\pi {\epsilon }_0}\cdot \frac{q_1}{a}=\frac{1}{4\pi {\epsilon }_0}\cdot \frac{q_2}{b}$
    or q1q2=ab$\frac{q_1}{q_2}=\frac{a}{b}$
    Now, the electric field on the two spheres is given as
    E1=14πε0⋅q1a2$E_1=\frac{1}{4\pi {\epsilon }_0}\cdot \frac{q_1}{a^2}$
    E2=14πε0⋅q2b2$E_2=\frac{1}{4\pi {\epsilon }_0}\cdot \frac{q_2}{b^2}$
    or E1E2=q1q2⋅b2a2=ab⋅b2a2=ba$\frac{E_1}{E_2}=\frac{q_1}{q_2}\cdot \frac{b^2}{a^2}=\frac{a}{b}\cdot \frac{b^2}{a^2}=\frac{b}{a}$
    Therefore, b : a is the ratio of the electric field of the first sphere to that of the second sphere. The surface charge densities of the two spheres are given as
    σ1=q14πa2${\sigma }_1=\frac{q_1}{4\pi a^2}$ (As the charges are distributed uniformly over the surfaces of conducting spheres)
    σ2=q24πb2${\sigma }_2=\frac{q_2}{4\pi b^2}$
    ∴σ1σ2=q1q2⋅b2a2=ab⋅b2a2=ba$\therefore \frac{{\sigma }_1}{{\sigma }_2}=\frac{q_1}{q_2}\cdot \frac{b^2}{a^2}=\frac{a}{b}\cdot \frac{b^2}{a^2}=\frac{b}{a}$
    Therefore, the surface charge densities are inversely related with the radii of the sphere. The surface charge density on the sharp and pointed ends of a conductor is higher than on its flatter portion since a flat portion may be taken as a spherical surface of large radius and a pointed portion as that of small radius.